LAWRA Tutorial
Linear Algebra with Recursive Algorithms
http://lawra.uni-c.dk/lawra/1
Jerzy Wasniewski2
UNI C
C
Danish IT3 Center for
Research and Education4
Technical University of Denmark,
Building 304, DK-2800 Lyngby, Denmark,
email: jerzy.wasniewski@uni-c.dk
A good quality numerical software is very important in many
industrial applications. Here "quality" means:
- the practical problem is solved as fast as possible,
- with minimum memory requirement (the memory is still
not large enough for scientific and industrial applications), and
- with an acceptable error (as is well-known computers
make roundoff errors which can spoil the result significantly).
Therefore, some companies develop libraries of computer
programs which are ready to use, and where the "best" present
algorithms are implemented. One such library is LAPACK (Linear
Algebra PACKage) [3] which is the basis for highly tuned
libraries on different architectures, and BLAS (Basic Linear
Algebra Subroutines) [7,4,5,16] in which
some basic matrix and vector operations are implemented, and
which is heavily used in LAPACK.
Modern computer architectures have a hierarchical memory (with 1
or more levels of cache memory). This allows faster algorithms
but only when the algorithm is designed appropriately. There is
some development in this field, for example in LAPACK [3]
and ATLAS (Automatically Tuned Linear Algebra
Software) [19], but it seems that the memory is not
used to the full possible extent, and there is a reason to do
further research.
In the last 4 years a new idea emerged which leads to faster
algorithms on modern processors. This is the recursive
formulation of all basic algorithms in numerical software
packages. It turns out that recursion leads automatically to
better utilization of the memory, and so faster algorithms
result. Sometimes better algorithms emerge. There is a number of
algorithms where recursion has successfully been applied, for
example
[9,10,11,1,14,12,13,18,2,8,6].
The recursion introduce a new data storage format by which the
BLAS Level 3 can be applied. For example, the new recursive
packed storage data format causes that the fast Cholesky
algorithm only requires 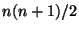 memory but not
memory but not
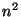 [1] (see Fig.
[1] (see Fig.![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) and
and
![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) in the Appendix), where
in the Appendix), where 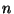 is an order of
the matrix. Figure
is an order of
the matrix. Figure ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) shows that the New Factorization Algorithm
for symmetric indefinite matrices with Bunch-Kaufman pivoting works not
slower than the LAPACK full storage algorithm, but using only
shows that the New Factorization Algorithm
for symmetric indefinite matrices with Bunch-Kaufman pivoting works not
slower than the LAPACK full storage algorithm, but using only
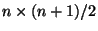 memory. The Figure
memory. The Figure ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) compares the
recursive
compares the
recursive 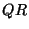 factorization (RGEQRF) with the LAPACK
factorization (RGEQRF) with the LAPACK 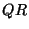 factorization
(DGEQRF). The recursive algorithms automatically benefit from
the parallelism while the traditional methods do not.
factorization
(DGEQRF). The recursive algorithms automatically benefit from
the parallelism while the traditional methods do not.
The second important issue is that recursive programs ``capture''
very concisely the mathematical formulation, and are easy to read
and understand (but only if one knows the subject area).
New research on recursive algorithms started at the IBM Watson
Research Center, USA in 1997 [17,15]. Then, in the
beginning of 1998, two more centers joined the team working on
these algorithms: UNI C (Danish Computing Center for
Research and Education), and the University of Umeå, Sweden.
University of Rousse (Bulgaria) was also involved for some time
in these algorithms. The ATLAS [19] library is extended
by the recursive algorithms. University of Tennessee at Knoxville
applied recursion to sparse matrix technique
[8,6].
C (Danish Computing Center for
Research and Education), and the University of Umeå, Sweden.
University of Rousse (Bulgaria) was also involved for some time
in these algorithms. The ATLAS [19] library is extended
by the recursive algorithms. University of Tennessee at Knoxville
applied recursion to sparse matrix technique
[8,6].
We have improved significantly some of the existing algorithms
in LAPACK (see Figures in the
Appendix). This happens because the recursive formulation uses
the cache memory more efficiently and sometimes also allows the
use of larger block operations (i. e. more efficient use of
BLAS).
There are many widely used algorithms in practice for which the
recursive formulation has not been studied (e. g. algorithms for
eigenvalues, singular values, generalized eigenvalues,
generalized singular values, etc.). Based on our preliminary
experience, we think that recursion will also benefit these
algorithms. predict that the of new numerical software
Another important consequence of this research is that as
computer vendors improve the hardware of parallel high
performance computers, the memory hierarchies are tending to
become deeper. Thus recursive algorithms, since they
automatically block for them, will be able to take advantage of
the new memories. In this way our research has impact on both
software and hardware.
- We give a very brief overview of the
Algorithms and Architecture Approach as a means to produce high
performance Dense Linear Algebra Algorithms. The key idea that we
develop is blocking for today's deep memory hierarchies.
- We develop how recursion relates to dense
linear algebra. Specifically we show how recursion leads to
automatic variable blocking. Clearly, variable blocking is more
general than conventional fixed blocking.
- We describe new data structures for full and
packed storage of dense symmetric/triangular arrays that
generalize both. Using the new data structures one is led to
several new algorithms that save ``half'' the storage and
outperform the current blocked based level 3 algorithms in
LAPACK.
- We will describe a recursive formulation of
Cholesky Factorization of a matrix in packed storage. The key to
this algorithm is a novel data structure that converts standard
packed format into
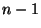 ``square'' full matrices and
``square'' full matrices and 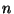 scalar diagonal elements. This formulation only use conventional
GEMM, a surprising result in itself.
scalar diagonal elements. This formulation only use conventional
GEMM, a surprising result in itself.
- Performance results for various dense linear
algebra algorithms will be presented for several different
computers. In particular, performance graphs of the LAPACK
Cholesky (full and packed storage) algorithms and our new
Cholesky algorithm using Recursive Packed Format will be
presented.
-
- 1
-
B. S. Andersen, F. Gustavson, and J. Wasniewski.
A Recursive Formulation of Cholesky Factorization of a
Matrix in Packed Storage.
Computer Science Dept. Technical Report CS-00-441,
University of Tennessee, Knoxville, TN, 2000.
Also LAPACK Working Note 441, and the paper is already accepted for
publication in TOMS of the ACM.
- 2
-
B.S. Andersen, F. Gustavson, A. Karaivanov, J. Wasniewski, and P.Y.
Yalamov.
LAWRA - Linear Algebra with Recursive Algorithms.
In R. Wyrzykowski, B. Mochnacki, H. Piech, and J. Szopa, editors,
Proceedings of the  International Conference on Parallel
Processing and Applied Mathematics, PPAM'99, pages 63-76, Kazimierz Dolny,
Poland, 1999. Technical University of Czestochowa.
International Conference on Parallel
Processing and Applied Mathematics, PPAM'99, pages 63-76, Kazimierz Dolny,
Poland, 1999. Technical University of Czestochowa.
- 3
-
E. Anderson, Z. Bai, C. Bischof, L. S. Blackford, J. Demmel, J. Dongarra,
J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen.
LAPACK Users' Guide.
Society for Industrial and Applied Mathematics, Philadelphia, PA,
third edition, 1999.
- 4
-
J. Dongarra, J. Du Croz, I. S. Duff, and S. Hammarling.
Algorithm 679: A set of Level 3 Basic Linear Algebra
Subprograms.
ACM Trans. Math. Soft., 16(1):18-28, March 1990.
- 5
-
J. Dongarra, J. Du Croz, S. Hammarling, and Richard J. Hanson.
Algorithm 656: An extended set of Fortran Basic Linear
Algebra Subroutines.
ACM Trans. Math. Soft., 14(1):18-32, March 1988.
- 6
-
J. Dongarra, V. Eijkhout, and P.
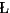 uszczek.
uszczek.
Recursive Approach in Sparse Matrix LU Factorization.
http://www.netlib.org/utk/people/JackDongarra/papers.html, 2000.
To appear in: Scientific Programming after the SGI'2000
Conference.
- 7
-
J. Dongarra et al.
BLAS (Basic Linear Algebra Subprograms).
http://www.netlib.org/blas/.
Ongoing Projects at the Innovative Computing Laboratory, Computer
Science Department, University of Tennessee at Knoxville, USA.
- 8
-
J. Dongarra and P. Raghavan.
A New Recursive Implementation of Sparse Cholesky
Factorization.
http://www.netlib.org/utk/people/JackDongarra/papers.html, 2000.
Submitted to IMACS 2000, Lausanne Switzerland.
- 9
-
E. Elmroth and F. Gustavson.
New Serial and Parallel Recursive 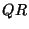 Factorization
Algorithms for SMP Systems.
Factorization
Algorithms for SMP Systems.
In B. Kågström, J. Dongarra, E. Elmroth, and
J. Wasniewski, editors, Proceedings of the 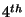 International
Workshop, Applied Parallel Computing, Large Scale Scientific and Industrial
Problems, PARA'98, number 1541 in Lecture Notes in Computer Science Number,
pages 120-128, Umeå, Sweden, June 1998. Springer.
International
Workshop, Applied Parallel Computing, Large Scale Scientific and Industrial
Problems, PARA'98, number 1541 in Lecture Notes in Computer Science Number,
pages 120-128, Umeå, Sweden, June 1998. Springer.
- 10
-
E. Elmroth and F. Gustavson.
Applying Recursion to Serial and Parallel QR
Factorization Leads to Better Performance.
IBM Journal of Research and Development, 44(4):605-624, 2000.
- 11
-
E. Elmroth and F. Gustavson.
High-Performance Library Software for 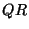 Factorization.
Factorization.
In T. Sørevik, F. Manne, R. Moe, and A.H. Gebremedhin, editors,
Proceedings of the  International Workshop, PARA'2000, Applied
Parallel Computing, number 1947 in Lecture Notes in Computer Science Number,
pages 53-63, Bergen, Norway, June 2000. Springer.
International Workshop, PARA'2000, Applied
Parallel Computing, number 1947 in Lecture Notes in Computer Science Number,
pages 53-63, Bergen, Norway, June 2000. Springer.
- 12
-
A. Gupta, F. Gustavson, A. Karaivanov, J. Wasniewski, and P. Yalamov.
Experience with a Recursive Perturbation Based Algorithm
for Symmetric Indefinite Linear Systems.
In I. Duff, editor, EuroPar'99 Conference Proceedings,
Toulouse, France, September 1999.
- 13
-
F. Gustavson, A. Karaivanov, M.I. Marinova, J. Wasniewski, and P. Yalamov.
A Fast Minimal Storage Symmetric Indefinite Solver.
In T. Sørevik, F. Manne, R. Moe, and A.H. Gebremedhin, editors,
Proceedings of the  International Workshop, PARA'2000, Applied
Parallel Computing, number 1947 in Lecture Notes in Computer Science Number,
pages 104-113, Bergen, Norway, June 2000. Springer.
International Workshop, PARA'2000, Applied
Parallel Computing, number 1947 in Lecture Notes in Computer Science Number,
pages 104-113, Bergen, Norway, June 2000. Springer.
- 14
-
F. Gustavson, A. Karaivanov, J. Wasniewski, and P. Yalamov.
A Columnwise Recursive Perturbation Based Algorithm for
Symmetric Indefinite Linear Systems.
In PDPTA'99 Conference Proceedings, Las Vegas, USA, June 1999.
- 15
-
F.G. Gustavson.
Recursion Leads to Automatic Variable Blocking for Dense
Linear-Algebra Algorithms.
IBM Journal of Research and Development, 41(6), November 1997.
- 16
-
C. L. Lawson, R. J. Hanson, D. Kincaid, and F. T. Krogh.
Basic Linear Algebra Subprograms for Fortran Usage.
ACM Trans. Math. Soft., 5:308-323, 1979.
- 17
-
S. Toledo.
Locality of Reference in LU Decomposition with Partial
Pivoting.
SIAM Journal of Matrix Analysis and Applications,
18(4):1065-1081, 1997.
- 18
-
J. Wasniewski, B.S. Andersen, and F. Gustavson.
Recursive Formulation of Cholesky Algorithm in Fortran 90.
In B. Kågström, J. Dongarra, E. Elmroth, and
J. Wasniewski, editors, Proceedings of the  International
Workshop, Applied Parallel Computing, Large Scale Scientific and Industrial
Problems, PARA'98, number 1541 in Lecture Notes in Computer Science Number,
pages 574-578, Umeå, Sweden, June 1998. Springer.
International
Workshop, Applied Parallel Computing, Large Scale Scientific and Industrial
Problems, PARA'98, number 1541 in Lecture Notes in Computer Science Number,
pages 574-578, Umeå, Sweden, June 1998. Springer.
- 19
-
R.C. Whaley and J. Dongarra.
ATLAS: Automatically Tuned Linear Algebra Software.
http://www.netlib.org/atlas/, 1999.
University of Tennessee at Knoxville, Tennessee, USA.
![\rotatebox {-90}{\scalebox{.40}{\includegraphics*[]{drpptrf.alpha.eps}}}](img13.gif)
![\rotatebox {-90}{\scalebox{.40}{\includegraphics*[]{drpptrs.alpha.eps}}}](img14.gif)
Figure:
Performance of the recursive Complex Hermitian
Cholesky factorization and solution on INTEL Pentium III, @ 500 MHz.
The recursive results include the time consumed by converting from
packed to recursive packed storage and vice versa. All routines call the
optimized ATLAS BLAS (ZGEMM).
![\rotatebox {-90}{\scalebox{.40}{\includegraphics*[]{zrpptrf.linux.eps}}}](img15.gif)
![\rotatebox {-90}{\scalebox{.40}{\includegraphics*[]{zrpptrs.linux.eps}}}](img16.gif) |
Figure:
Performance of the new factorization algorithm
where the matrices are symmetric indefinite with Bunch-Kaufman pivoting
on an SGI Origin 2000, R12000 @ 300 MHz, using the Atlas BLAS library.
![\rotatebox {-0}{\scalebox{.80}{\includegraphics*[]{f_sgi_nb40_n50_3000_10_a.eps}}}](img17.gif) |
Figure:
Recursive QR factorization. Uniprocessor
performance on a 200 MHz IBM POWER3 node.
![\rotatebox {-0}{\scalebox{.80}{\includegraphics*[]{rgeqrfpw3.eps}}}](img18.gif) |
LAWRA Tutorial
Linear Algebra with Recursive Algorithms
http://lawra.uni-c.dk/lawra/1
This document was generated using the
LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_navigation -split 0 -white jerzysorento01.tex
The translation was initiated by Kenneth Tan on 2001-05-16
Footnotes
- ... http://lawra.uni-c.dk/lawra/1
- The LAWRA Website has not been updated for the last two years.
The tutorial contains much newer material than the Website.
- ... Wasniewski2
- Collaborations:
Fred Gustavson, Bjarne S. Andersen, Minka I. Marinova,
Alexander Karaivanov, Ivan Lirkov and Plamen Yalamov
- ... IT3
- Information Technology
- ... Education4
- Previously: Danish Computing
Center for Research and Education
Kenneth Tan
2001-05-16
![]() C
C
![]() memory but not
memory but not
![]() [1] (see Fig.
[1] (see Fig.![]() and
and
![]() in the Appendix), where
in the Appendix), where ![]() is an order of
the matrix. Figure
is an order of
the matrix. Figure ![]() shows that the New Factorization Algorithm
for symmetric indefinite matrices with Bunch-Kaufman pivoting works not
slower than the LAPACK full storage algorithm, but using only
shows that the New Factorization Algorithm
for symmetric indefinite matrices with Bunch-Kaufman pivoting works not
slower than the LAPACK full storage algorithm, but using only
![]() memory. The Figure
memory. The Figure ![]() compares the
recursive
compares the
recursive ![]() factorization (RGEQRF) with the LAPACK
factorization (RGEQRF) with the LAPACK ![]() factorization
(DGEQRF). The recursive algorithms automatically benefit from
the parallelism while the traditional methods do not.
factorization
(DGEQRF). The recursive algorithms automatically benefit from
the parallelism while the traditional methods do not.
![]() C (Danish Computing Center for
Research and Education), and the University of Umeå, Sweden.
University of Rousse (Bulgaria) was also involved for some time
in these algorithms. The ATLAS [19] library is extended
by the recursive algorithms. University of Tennessee at Knoxville
applied recursion to sparse matrix technique
[8,6].
C (Danish Computing Center for
Research and Education), and the University of Umeå, Sweden.
University of Rousse (Bulgaria) was also involved for some time
in these algorithms. The ATLAS [19] library is extended
by the recursive algorithms. University of Tennessee at Knoxville
applied recursion to sparse matrix technique
[8,6].
![\rotatebox {-90}{\scalebox{.40}{\includegraphics*[]{drpptrf.alpha.eps}}}](img13.gif)
![\rotatebox {-90}{\scalebox{.40}{\includegraphics*[]{drpptrs.alpha.eps}}}](img14.gif)
![\rotatebox {-90}{\scalebox{.40}{\includegraphics*[]{zrpptrf.linux.eps}}}](img15.gif)
![\rotatebox {-90}{\scalebox{.40}{\includegraphics*[]{zrpptrs.linux.eps}}}](img16.gif)
![\rotatebox {-0}{\scalebox{.80}{\includegraphics*[]{f_sgi_nb40_n50_3000_10_a.eps}}}](img17.gif)